Due to the high coupling constant of the magnetic monopole perturbative calculations of the magnetic monopole cross section cannot be made. Instead a Drell-Yan mechanism is assumed for the cross section calculation. These two diagrams shows annihilation of the quark-antiquark via the intermediate virtual photon and later photon decay into the two leptons (left) and monopole-antimonopole pair (right).

We can use this formulation to attempt to calculate the production cross-section for magnetic monopoles once the proper coupling of the magnetic charge to the electromagnetic field is incorporated. This is derived by combining the Dirac quantization condition with the definition of the coupling constant α_mm = (ng_D/e) ( α ∼ e2), which gives the cross-section:

 

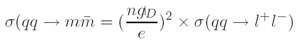
For pp collisions there exists data on the differential cross-section for production of massive virtual photons, which exhibits scaling and falls of exponentially with x ≡ 2M_m/√s, where √s is the available centre-of-mass energy and M_m is the magnetic monopole mass. To this end we have predicted monopole-pair cross-sections at LHC energies by the formula:

 

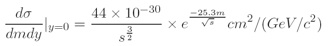
To obtain the cross-section for monopole pair production with mass M = (s/2)1/2 we integrate the cross-section above m = 2M_m. Assuming no phase space suppression:

 

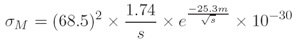
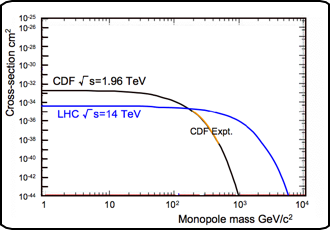
The cross-section given above is intended to be a rough point of reference cross-section for the production of magnetic monopoles via the electromagnetic interaction. This estimate is conservative since higher order diagrams with more than one virtual photon in the intermediate state will also contribute. Production via gluon-gluon fusion may be more likely still. We find excellent agreement with the Drell-Yan curve for the mass interval 200-600 GeV/c2 published by the authors of the CDF experiment [34], as is shown by the orange curve which fits the black predicted curve well.